Este é um breve relato sobre uma experiência que fiz na minha turma de 6º ano no Colégio Municipal Nossa Senhora das Graças – Mangaratiba, sobre uma atividade relacionada a padrões. Objetivando auxiliar no desenvolvimento do pensamento algébrico segundo Radford (2014). A atividade aplicada foi retirada do artigo de Canavarro (2007).
Este é um breve relato sobre uma experiência que fiz na minha turma de 6º ano no Colégio Municipal Nossa Senhora das Graças – Mangaratiba, sobre uma atividade relacionada a padrões. Objetivando auxiliar no desenvolvimento do pensamento algébrico, segundo as pesquisas de Radford (2014). A atividade aplicada foi retirada do artigo de Canavarro (2007).
A Atividade
A atividade, aplicada em abril de 2016, foi a seguinte:
Questões aplicadas na atividade
1) Temos 5 amigos que ganharam um concurso. Ao saberem a notícia, telefonaram uns para os outros para se parabenizarem. É possível descobrir quantas ligações tiveram que fazer os cinco amigos para falarem uns com os outros?
2) E se fossem 6 amigos, quantas ligações seriam feitas?
3) E 7 amigos fariam quantas ligações?
4) É possível descobrir alguma regra para um número qualquer de amigos? Podes encontrá-la? Utilize a regra encontrada para descobrir a quantidade de ligações feita por 20 amigos.
Nosso objetivo
O objetivo era o de induzir os alunos a identificarem a existência de termos desconhecidos (nesse caso, a quantidade de ligações e uma quantidade qualquer de amigos), nomearem essas quantidades utilizando uma linguagem apropriada a sua idade e trabalharem com essas quantidades como se fossem termos conhecidos. Com isso, segundo Radford (id ibid), eles estariam desenvolvendo o pensamento algébrico.
Podemos afirmar que para descobrir uma regra para a quantidade de ligações para uma quantidade qualquer de amigos, pode-se utilizar um pensamento puramente aritmético, envolvendo as tentativas com as quantidades de amigos dadas, mas também pode-se chegar a uma generalização, que está relacionada ao pensamento algébrico de RADFORD, pois ao nomear as quantidades desconhecidas e trabalhar com elas como conhecidas está se fazendo uma generalização.
Quem participou da atividade?
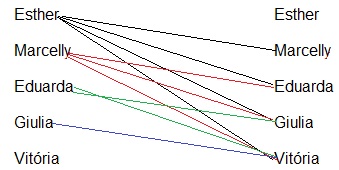
A turma era constituída de 24 alunos que foram divididos em grupos de 4. Escrevi a atividade na lousa e deixei-os à vontade para resolver como achassem melhor, contanto que dialogassem com os integrantes do seu próprio grupo. Eles se interessaram e se empenharam na resolução. Todos os grupos conseguiram resolver as questões 1 a 3. Houveram tentativas erradas, discussões, pedidos de ajuda a professora, novas tentativas e então cada grupo foi ao quadro explicar suas resoluções. Abaixo duas imagens (figuras 1 e 2) que representam as soluções de dois dos grupos (1 e 2) para a quantidade de ligações feitas por 5 amigos.
Figura 1: Solução do grupo 1
Figura 2: Solução do grupo 2
Analisando as respostas dos alunos
O grupo 1 somou 4+3+2+1 encontrando como resposta 10 ligações e fizeram o mesmo esquema para as quantidades maiores e afirmaram que para encontrar a quantidade de ligações feitas por 20 amigos bastava somar todos os números anteriores a 20, 19+18+17+...+3+2+1 e encontraram 190 ligações. Eles então, generalizaram dessa forma: “é só a gente somar todos os números que vem antes da quantidade de amigos.”
O grupo 2 foi o primeiro a apresentar na lousa sua solução. Era um grupo só de meninas. Elas afirmaram que 5 amigas fariam 25 ligações. Mesmo não sendo o resultado correto, me chamou atenção o esquema feito por elas. Após observarem que a maior parte dos grupos encontrou 10 ligações para 5 amigos elas me questionaram se o delas estava errado ou os outros. Então falei para elas que a quantidade correta de ligações feitas pelos 5 amigos era realmente 10. E instiguei-as a pensar um pouco mais sobre o esquema que fizeram. Depois de um tempo elas apresentaram o mesmo esquema (figura 3), porém com algumas modificações.
Figura 3: Nova solução do grupo 2
Foram ao quadro e desenharam o primeiro esquema que haviam feito (figura 2) e este novo esquema (figura 3). Explicaram o seguinte:
“Uma amiga não liga para ela mesma, então diminuímos 5 ligações. Percebemos também que as ligações estavam sendo contadas 2 vezes cada uma. Tiramos as flechas duplicadas e ficamos com 10 ligações. ”
Fizeram este novo esquema (figura 3) para as outras quantidades de amigos e encontraram as respostas corretas. Generalizaram da seguinte maneira:
“Basta a gente pegar a quantidade de amigos vezes a quantidade de amigos, diminuir a quantidade de amigos e depois dividir por 2. ”
Observações acerca das respostas
Em ambos os casos observamos a presença do pensamento aritmético com suas tentativas, erros e acertos. Com números conhecidos. Porém no segundo caso, das meninas, observamos algo mais profundo do que o pensamento aritmético, pois elas identificaram a quantidade desconhecida e nomearam como “quantidade de amigos” e fizeram uma generalização avançadíssima para o ano escolar no qual se encontravam:  em nossa linguagem formal.
em nossa linguagem formal.
 em nossa linguagem formal.
em nossa linguagem formal.
Considerações Finais
Elas não trabalharam com as quantidades desconhecidas como sendo conhecidas, porém demostraram um grau superior de pensamento matemático, através de sua generalização.
Foi gratificante observar que uma atividade talvez considerada simples gerou resultados tão bons como, o diálogo entre eles, o empenho em resolver algo juntos, o saber ouvir a opinião do amigo e levá-la em consideração e o desenvolvimento de um tipo de pensamento algébrico ao identificar padrões, fazer argumentações e generalizações, conforme Canavarro (id ibid)
Que nós, como educadores matemáticos, possamos não nos prender somente ao ensino mecanizado da matemática, mas que possamos trabalhar com os nossos alunos atividades que os levem a se desenvolverem como pessoas, como cidadãos. Sabendo pensar, argumentar, fazer escolhas, ouvir e respeitar o outro, enfim, viver em sociedade como um cidadão pleno, conforme orientações da LDB em seu 2º parágrafo afirmando que a educação “[...] tem por finalidade o pleno desenvolvimento do educando, seu preparo para o exercício da cidadania e sua qualificação para o trabalho. ” (BRASIL, 1996, p.1)
Referências
BRASIL. Ministério da Educação. Lei de Diretrizes e Bases da Educação Nacional – LDB. 14ª edição. Brasília, DF, 2016.
CANAVARRO, A. P. O Pensamento Algébrico na Aprendizagem da Matemática nos Primeiros Anos. Quadrante, vol. XVI, nº 2, 2007.
RADFORD, L. The Progressive Development of Early Embodied Algebraic Thinking. Mathematics Education Research Journal [1033-2170] Radford, Luis yr:2014 vol:26 iss:2 pp:257 -277.
Este é um artigo convidado. Foi escrito e enviado por Marcela Caetano, professora da SMEM.