Esta atividade já foi aplicada em diversas turmas nas prefeituras do Rio de Janeiro, Nova Iguaçu e Duque de Caxias. Em todas as aplicações verificamos o aumento do engajamento dos alunos e por conseguinte proporcionando o aprendizado efetivo do tema proposto.
O presente artigo traz uma nova possibilidade para aulas de matemática através da utilização da tecnologia. Nessa construção no Geogebra, chamada de Applet, desenvolvemos um jogo (Figura 1) para que os alunos encontrassem as raízes de equações do 2º grau.
Esta atividade já foi aplicada em diversas turmas nas prefeituras do Rio de Janeiro, Nova Iguaçu e Duque de Caxias. Em todas as aplicações verificamos o aumento do engajamento dos alunos e por conseguinte proporcionando o aprendizado efetivo do tema proposto.
 |
| Figura 1 |
Metodologia
Os alunos são organizados em equipes (TBL – Team Based Learning), separando os mesmos em grupos de 5 ou 6 membros para o desenvolvimento, debate e resolução das equações (Figura 2), cada qual deverá receber uma folha para entregar ao professor a cada rodada as suas resoluções.
 |
| Figura 2 |
Para começar o jogo devemos clicar em “Nova Equação” (Figura 3) e a primeira equação já estará disponível para todos os grupos, o tempo então, começará a contar e todos terão 2 minutos para entregar a folha com a resolução ao professor.
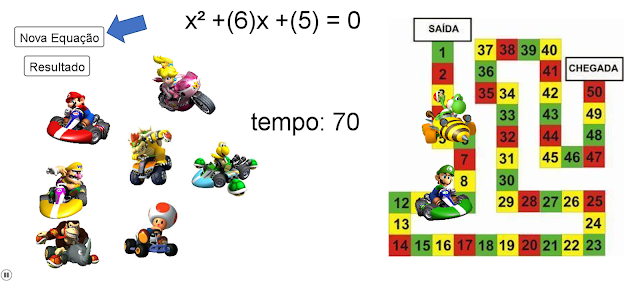 |
| Figura 3 |
Quando todos entregarem ou se o tempo atingir 120 segundos ou outro tempo combinado com os alunos, cabe ao docente clicar em “Resultado” para encerrar a rodada, o próprio jogo fornecerá para a turma o feedback sobre a questão (Figura 4) e a quantidade de casas que devem andar os personagens dos grupos que acertarem as raízes. Dúvidas sobre as resoluções e levantamentos com considerações podem ser feitos nesse momento afim de eliminar as dúvidas para as próximas rodadas.
 |
| Figura 4 |
O processo deve ser repetido até o final do tempo de aula, caso algum grupo alcance a linha de chegada, a atividade está encerrada, caso não, o jogo digital oferece essa vantagem em relação ao manual, de se gravar o desenvolvimento e de se retornar posteriormente em um nova oportunidada e do ponto exato de término da aula anterior (Figura 5).
 |
| Figura 5 |
Com relação a avaliação podemos utilizar e pontuar as soluções dos alunos, pois chegamos no término da aula com tudo corrigido podendo acrescentar uma pontuação extra as colocações de cada grupo.
Vídeo da atividade
Vídeo da atividade: Neste link!!!!
Considerações Finais
Aos colegas professores que estão lendo este trabalho como aplicamos para turmas do 9º ano do ensino fundamental II, tivemos a preocupação no processo de construção que as raízes fossem números inteiros no intervalo [-9,9]. Sabemos da importância de trabalharmos com os números Reais, mas deixarmos o código aberto caso queira alterar e aplicar em turmas de outros anos de escolaridade.
Desta forma, percebemos ao longo do processo que os alunos participaram efetivamente da atividade e em cada rodada procuravam minimizar os erros para através de uma competição sadia cruzarem a linha de chegada.O feedback recebido foi muito bom, os grupos mostraram muita união e comprometimento na resolução dos exercícios tentando alcançar a vitória, mas sabemos que a mesma se deu ao tirarmos muitos discentes da inércia transformando-os em atores do seu próprio aprendizado.
Este é um artigo convidado. Foi escrito e enviado por Rafael Costa, professor da SMERJ e UNISUAM e Leandro Nascimento, professor da SMEDC e da UNESA.






